031 - PJ Sutherland - The Complementary Dynamics of Mean Reversion and Trend-Following Strategies
Behavioural Biases, Statistics that Lie, Leptokurtic Distributions, Black Swans … and what to do about them
In the domain of quantitative finance, the juxtaposition of mean reversion and trend-following strategies constitutes a pivotal dialogue in the formulation of robust trading paradigms. Each methodology is underpinned by unique theoretical and empirical foundations, presenting distinct opportunities and inherent vulnerabilities. However, when synthesized within a cohesive portfolio framework, these strategies reveal a profound synergy that not only enhances diversification but also attenuates systemic risks. This discourse delves into the nuances of each strategy and elucidates their integrative potential.
Behavioural Biases
An article from Fidelity here suggests that many investors in Peter Lynch’s Magellan Fund (which returned around 30%pa for more than a decade) would have lost money. Why? They refer to market research which demonstrates the average holding period for equity mutual funds is less than three years. Investors pile in when funds are doing well and exit in draw downs. By doing this they limit their upside and then crystalize their draw downs.
Likewise, traders are not immune to the emotions of fear and greed and can do exactly the same thing with their trading models.
I mention this because it highlights the difficulty in making quantitative decisions, and more than that, even if attempting to ‘statistically validate’ one’s decisions, the lack of sufficient data or a tendency to torture what data is there, can lead to generating statistics which are meaningless. On the episode with Jason Buck we talked about ergodicity (sequencing risk) and he brought up some great, easy to understand examples of how common statistics can give us the wrong idea. In the case of Peter Lynch, the average return is completely different if you enter and exit at different times.
Revisiting the Foundations of Financial Data: Beyond Normal Distributions
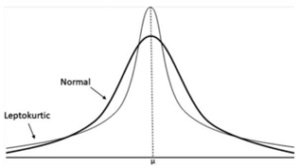
Traditional financial models often assume that asset prices and returns follow a normal distribution. However, extensive empirical evidence reveals that financial markets exhibit fat tails, skewness, and kurtosis—characteristics that deviate significantly from normality. Events such as market crashes or meteoric surges, termed outliers, occur far more frequently than the Gaussian model predicts, invalidating assumptions that underlie many risk management and valuation models. Furthermore, there is more mean reverting activity than a normal distribution would suggest.
The implications of these non-normal distributions are profound. Trading strategies that ignore the reality of fat-tailed, and higher-peaked, distributions risk underestimating the frequency and magnitude of extreme events, and also the prevalence of mean-reversion. Models premised on normality fail to account for the clustering of volatility and the disproportionate influence of outliers—an oversight that can lead to catastrophic mispricing of risk.
Take any stock over the last 10 years and look at the distribution of its returns. No doubt you’ll see a high degree of small gyrations around a mean, and also, insanely large highs and lows that are 6 standard deviations away from the mean. The probability of these returns, if assuming normality, are frighteningly tiny, yet there they are. The higher peaks and fatter tails of the leptokurtic distribution makes for trading opportunities in an inefficient market, but these opportunities will have distinct risks. If we are using metrics (and thinking) based on normal distributions, we will not build the right risk management toolkit for our particular trading strategies. A good case can be made that human behaviour is a core component driving these market anomalies.
The leptokurtic versus the normal distribution
So how does this relate to the trading at Sutherland Capital Management? Let's dig into the core components of the portfolio.
Mean Reversion Strategies: Foundations, Advantages, and Limitations
Mean reversion strategies operate on the premise that asset prices exhibit a central tendency, reverting to a statistically defined mean over time. The detection of deviations from this mean provides a basis for contrarian trading opportunities.
Strengths
Prevalence of Opportunities: Short-term trading means lots of opportunities to compound wealth, manage risk and statistically validate. Incredible wealth can be compounded in this manner, but many will simply ‘warehouse risk’ along the way, until the uninsured warehouse catches fire.
High Win Rate: Ego aside, high win rates (even with small wining amounts) with high frequency trading, generate the compounding of wealth. Low win rates and big wins can do the same of course.
Predictable Performance: Under stable market regimes, these strategies exhibit consistent returns, often characterized by superior Sharpe ratios. Nobody wants to finish the year negative.
Limitations:
Exposure to Tail Events: Structural market dislocations, such as systemic crises, may result in protracted deviations from the mean, culminating in substantial losses, and of course, a large enough ‘event’ is career destroying. Risk of ruin must be zero for any trader. So the only way to trade mean reversion is if one can confidently state that their risk of ruin is zero. This is far more difficult to achieve with mean reversion trading than with trend following.
Cutting Winners Short: These strategies relying on capturing small profits, using targets, and thus miss big outlier moves that can dramatically improve your equity balance. It can be frustrating in a raging bull market regime to miss out on some of those massive wins that are available. Statistically, it makes sense to try and capture these outliers if we want to beat the market. Of course, high frequency traders and market makers are an exception, playing at such a short timeframe that the compounding is incredible, and risks can more easily be contained / hedged.
Less Reliance on Stops: Stop losses may be ineffective when markets gap, and this can have a much bigger influence on a shorter-term strategy, given position sizes will be larger.
Commission Drag: Shorter term strategies are far more reliant on low commissions.
Execution: It’s likely that specific infrastructure will be needed to handle execution, particularly if one is trading a large number of sub-strategies. With more strategies comes the requirement for a larger capital balance as well.
Short-Term Trend-Following Strategies: Principles, Advantages, and Constraints
Trend-following strategies exploit momentum phenomena, seeking to capitalize on sustained directional movements. Entry points are typically identified following periods of price consolidation (perhaps less so with longer-term strategies), with positions held to capture the entirety of the trend. Cutting losses short and letting profits run gives us the opposite return profile of mean reversion. We go from negatively skewed strategies (higher chance of a seriously negative event) to positively skewed strategies (a few really big winners that carry many small losers, but no extreme losers). Doing this on a shorter-term timeframe (say 5 to 30 days) is not easy in the stock market.
Strengths:
Performance During Crises: These strategies excel in capturing large price movements during tail events, often acting as a hedge against systemic downturns. Of course, you’ll need to have deployed short strategies as well as long. They will act as a natural hedge against mean reversion positions.
Positive Skewness: Trend-following yields a performance profile characterized by infrequent but substantial gains, providing asymmetry in return distributions. The benefit of this cannot be understated. Positive skew means ‘staying alive’, it also means you want to be on the really big moves. The frequency of these events is less, sure, but if you’re willing to ‘take the medicine’ of lumpy returns, and hold on for the ride, your account balance is going to thank you.
Limitations:
Low Frequency of Success: Despite the magnitude of winning trades, the overall success rate of trend-following strategies tends to be modest. Extended periods of under-performance are possible.
Sensitivity to Market Noise: Choppy or range-bound markets can precipitate frequent whipsaws, eroding profitability in the short term.
Execution Complexity: For the short-term break-out trading that PJ does, there are significant execution difficulties. Slippage becomes the ‘devil in the detail’. Capturing momentum-driven profits necessitates sophisticated execution frameworks to minimize slippage and latency.
The Holy Grail: Synergizing Mean Reversion and Trend-Following Strategies
The integration of mean reversion and trend-following strategies within a single portfolio exploits their inherent complementarities. Trend-following strategies excel in capturing outliers—those rare, extreme price movements that defy normality—while mean reversion strategies capitalize on the more frequent, smaller fluctuations around equilibrium.
Even more significantly, PJ has purpose-built each ‘leg’ of this portfolio to work in unison. The idea is to maximise the non-correlation and ensure that the one strategy is a hedge for the other. PJ maintains essentially thousands of micro-strategies across long and short mean-reversion, as well as long and short trend-following (shorter term break-outs), across a highly diversified set of models/parameters. Doing this on the right universe, with the right execution software and you have an absolutely incredible trading machine. Every last cog and wheel in PJ’s engine is finely tuned, constructed from class-A materials, and not a drop of oil is wasted.
If it’s not already obvious, what he has achieved here is a level of non-correlation between return-streams that is hard to replicate. The result is:
Enhanced Resilience: The non-linear dynamics of trend-following buffer portfolios against the negative skewness of mean reversion, mitigating the impact of tail events. The mean-reversion strategies are already deployed in a very low-risk framework, with tiny bet sizes and a throttling ‘over the mean reversion curve’. Adding the break-out hedge strategies is the icing on the cake.
Broad Opportunity Set: By diversifying across contrasting paradigms, we can capture a wider array of market phenomena, reducing exposure to any single regime. There are many alphas being captured, and in the most efficient manner possible.
Improved Consistency: Combining strategies balances the high-frequency gains of mean reversion with the occasional windfall profits of trend-following, stabilizing returns. This is especially the case when deploying these strategies on the shorter timeframes!
Summary
The synthesis of mean reversion and trend-following strategies epitomizes the strategic advantage of diversification in portfolio management. By harmonizing these methodologies, practitioners can construct portfolios that are inherently robust, adaptive, and resilient across diverse market regimes. As financial markets evolve, the thoughtful integration of these paradigms will remain an essential tenet of advanced quantitative trading. However, the continued reliance on metrics grounded in flawed assumptions, such as the Sharpe ratio, highlights a broader irony within the financial industry - investors and traders can fall into simple traps of assessing risk and reward with faulty tools, or let behavioural biases misguide them.
I trust that this has highlighted the benefits of diversification, of shorter timeframes (but why not diversify with longer timeframes too!), of correct execution, and of a multi-model approach. Traders can return to simplicity in their models when the portfolio is tuned correctly. Furthermore, it is incredibly important to have the right thesis, a good understanding of statistics and a good grip on behavioural biases to generate a smart portfolio. You’ll probably never look at a Sharpe ratio the same way again. The markets are more complex than any one metric can ever hope to summarize!
Trade Well and Prosper!